Home

Welcome to the web pages of the Keccak Team!

In these pages, you can find information about our different cryptographic schemes and constructions, their specifications, cryptanalysis on them, the ongoing contests and the related scientific papers.

Latest news

  • Crunchy Contest: first 5-round pre-image challenge solved!

    We congratulate Xiaoen Lin, Hongbo Yu, Enming Dong, Wenhao Wu and Yantian Shen of Tsinghua University and of The National Research Center of Parallel Computer Engineering and Technology, Beijing, China, for solving the 5-round pre-image challenge on Keccak[r=640, c=160].

    It is the first time that a 5-round pre-image challenge of our crunchy contest is solved! The solution to the present challenge spans 27 blocks and was obtained using internal differential cryptanalysis involving symmetric states. The team reports a total complexity of about 261 5-round Keccak-f calls. The experiment was completed in around 7 days using 3000 core-groups on the new Sunway supercomputer! More details can be found in the slides that Xiaoen presented at PBC 2025.

  • RFC 9861: TurboSHAKE and KangarooTwelve

    Halving the number of rounds in a primitive is quite unusual, if not unprecedented. Do you imagine shortening AES-128 from 10 down to 5 rounds? Dividing by two the number of steps in SHA-256? Using a 128-bit elliptic curve instead of Ed/X25519? Or cutting in half the dimensions of the ring in ML-KEM? In these cases, the security would be seriously questioned or even fall apart completely.

    RFC 9861 defines two families of extendable output functions, both based on the Keccak-p[1600] permutation with 12 rounds, while the original SHA-3 and SHAKE family uses 24 rounds. Such a drastic reduction in the number of rounds may seem frightening, yet there is ample evidence from third-party cryptanalysis that 12 rounds provides a comfortable safety margin. For instance, the best collision attack reaches only 6 rounds. Despite its relative young age (it was first published in 2008), Keccak has been heavily scrutinized: The number of scientific papers that analyze it is higher than any other (unbroken) hash function!

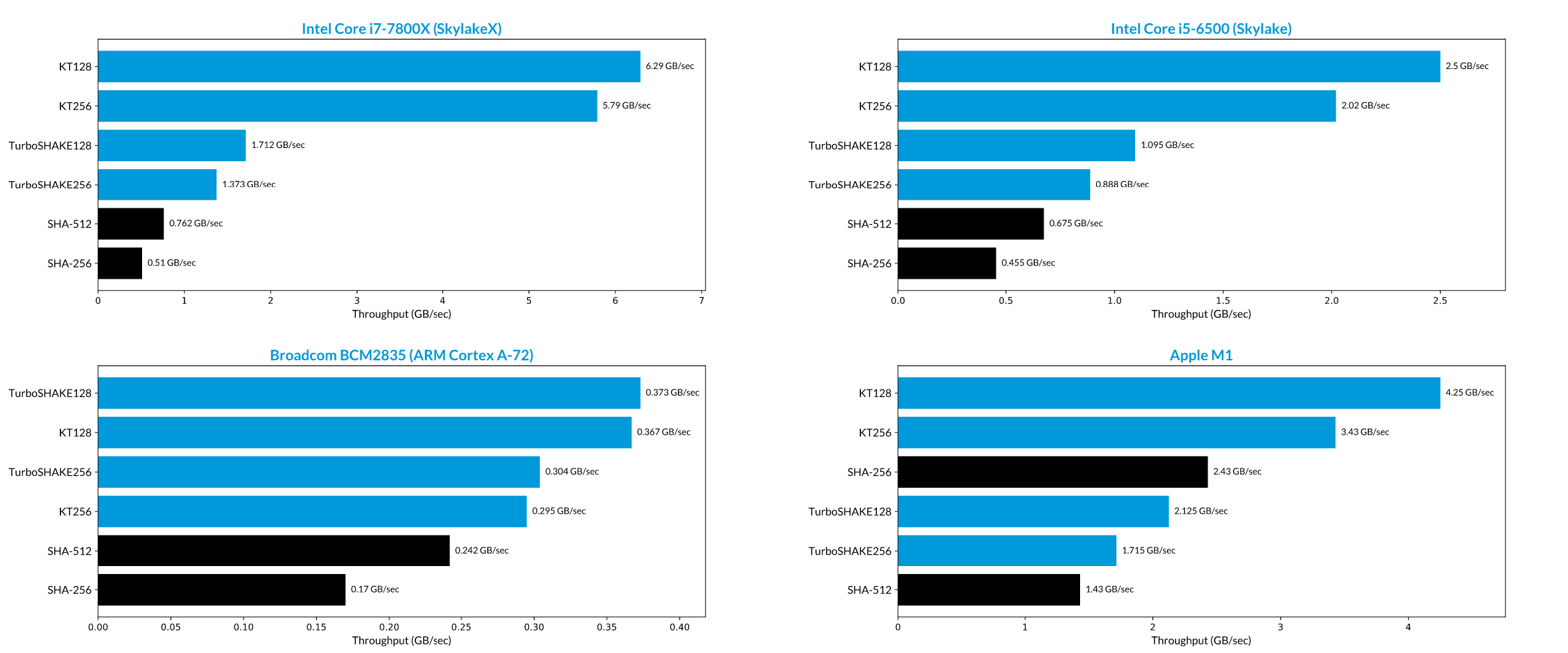
    By halving the number of rounds, TurboSHAKE128 and TurboSHAKE256 hash twice as fast as SHAKE128 and SHAKE256, respectively. KT128 and KT256 further build upon these by adding parallelism to speed up the implementations even more. As a result, these functions are blazing fast, both in software and in hardware.

    Speed measurements of TurboSHAKE and KangarooTwelve on various machines compared to SHA-2

    In the charts above, we show the throughput of the four functions defined in RFC 9861, plus SHA-256 and SHA-512, on four different processors. The Apple M1 has hardware acceleration for SHA-2 and SHA-3, which is used in our benchmark.

    We first proposed KT128 in 2016 under the name KangarooTwelve. We then proposed it to the the Crypto Forum Research Group (CFRG) as an RFC draft in 2017. This was the start of a long process. TurboSHAKE is the sponge function underlying KangarooTwelve, but it got that name only in 2023, as we found it was an interesting function on its own. KangarooTwelve was then instantiated in two security levels, KT128 and KT256. Finally, the RFC was officially published in October 2025.

  • Crunchy Contest: new 4-round pre-image challenge solved!

    We congratulate Xiaoen Lin, Hongbo Yu, Chongxu Ren, Zhengrong Lu and Yantian Shen of Tsinghua University, Beijing, China, for solving the 4-round pre-image challenge on Keccak[r=240, c=160].

    The previous pre-image challenge on the 400-bit version was solved on 3 rounds by Yao Sun and Ting Li in 2017. The solution to the present challenge was obtained using a meet-in-the-middle (MitM) involving symmetric states. The team reports a total complexity of about 258.7 4-round Keccak-f calls. It took about 4 days on the Sunway TaihuLight supercomputer using 10 thousand cores!

  • Crunchy Contest: new challenges solved!

    Started in June 2011, the Crunchy Contest proposes concrete collision and pre-images challenges based on reduced-round Keccak. After about 13 years, it is still active and the recent months have seen new challenges being solved. Hence, we would like to congratulate the authors of the latest solutions:

    • We congratulate Xiaoen Lin1, Hongbo Yu1, Zhengrong Lu1 and Yantian Shen1 for solving the 2-round pre-image challenge on Keccak[r=40, c=160].

      The previous pre-image challenge on the 200-bit version was solved on 1 round by Joan Boyar and Rene Peralta in 2013. This present challenge was solved by combining linear structures and symmetries within the lanes and exploiting sparsity of the round constants.

    • Furthermore, we congratulate Xiaoen Lin1, Hongbo Yu1, Congming Wei2, Le He3 and Chongxu Ren1 for solving the 4-round pre-image challenge on Keccak[r=640, c=160].

      The previous pre-image challenge on the 800-bit version was solved on 3 rounds by Jian Guo and Meicheng Liu in 2017. The solution to the present challenge was made possible by a number of optimizations related to linear structures and made use of mixed-integer linear programming (MILP). The team reports a total complexity of 260.9 4-round Keccak-f calls.

    • Finally, we congratulate Andreas Westfeld4 for solving the 2-round collision challenge on Keccak[r=40, c=160].

      The previous collision challenge on the 200-bit version was solved on 1 round by Roman Walch and Maria Eichlseder in September 2017. The solution to the present challenge targets the rounds 3 and 4 specifically, as it exploits the round constant that is zero for ir=3 in the 200-bit version.

    1. Department of Computer Science and Technology, Tsinghua University, Beijing, China
    2. Beijing Institute of Technology, Beijing, China
    3. School of Cyber Engineering, Xidian University, Xi'an, China
    4. Faculty of Informatics/Mathematics, HTW Dresden, Germany
  • Tighter trail bounds for Xoodoo

    Looking back at 2022, we further improved the bounds of differential and linear trails in Xoodoo. In the article Tighter trail bounds for Xoodoo available on the IACR Cryptology ePrint Archive, we report on the outcome of our new trail scan effort. The importance of trail bounds is not to be repeated; instead we refer to last year's news item for a discussion. As you can see in the table below, the lower bounds have been quite significantly improved.

    Next to a description of the optimizations in our trail search code that allowed us to improve the bounds, in the article we also report on a set of trails that are extendable to an arbitrary number of rounds and as such provide upper bounds for the minimum weight of trails. We summarize the new lower and upper bounds for the weight of trails in the table below. The bounds are the same for differential and linear trails.

    # rounds 1 2 3 4 5 6 8 10 12
    Lower bounds 2 8 36 80 98 132 176 220 264
    Upper bounds 2 8 36 80 120 168 288 440 624

News archives