Complete text in PDF format: Cryptographic sponge functions

In the context of cryptography, the sponge construction is a mode of operation, based on a fixed-length permutation (or transformation) and on a padding rule, which builds a function mapping variable-length input to variable-length output. Such a function is called a sponge function. It takes as input an element of $\mathbb{Z}_2^*$, i.e., a binary string of any length, and returns a binary string with any requested length, i.e., an element of $\mathbb{Z}_2^n$ with $n$ a user-supplied value. A sponge function is a generalization of both hash functions, which have a fixed output length, and stream ciphers, which have a fixed input length. It operates on a finite state by iteratively applying the inner permutation to it, interleaved with the entry of input or the retrieval of output.

Our original motivation for introducing the sponge construction was to serve as a reference for expressing security claims. Protocols or modes of hash functions are often proven secure in the random oracle model, i.e., assuming the hash function is a random oracle. The random oracle is an abstract primitive with the best possible cryptographic properties: it returns for every possible query a random (infinite) string. In practice, concrete hash functions are used instead and hence the security requirement they must satisfy is to behave like a random oracle. All known practical hash functions operate in an iterated way using finite memory. This may give rise to internal collisions: different inputs leading to the same internal state and consequently to the same output. This property is absent in a random oracle and so no hash function with finite memory can behave like a random oracle. Alternatively, applying the sponge construction with a random permutation results in a so-called random sponge. It turns out that a random sponge is as strong as a random oracle, except for the effects induced by the finite memory. Random sponges are thus well suited to replace random oracles for expressing security claims.

Additionally, the sponge construction and its sister construction, called the duplex construction, can be used to implement a wide spectrum of symmetric cryptography functions. This includes hashing, reseedable pseudo random bit sequence generation, key derivation, encryption, message authentication code (MAC) computation and authenticated encryption. The fundamental cryptographic primitive underlying all this is a fixed-length permutation. These permutation-based modes form efficient alternatives for the current block-cipher dominated cryptographic practice. On top of its conceptual elegance, a permutation has the advantages that it does not have a key schedule and that its inverse does not need to be implemented or efficient.

Roots

The idea of developing sponge functions came during the design of RadioGatún. This cryptographic hash function has a variable-length input and a variable-length output. When we proposed RadioGatún, we faced the problem that we had to express a claim of cryptographic security. For a hash function with fixed output length $n$, one usually implicitly or explicitly claims its security to be as good as a random oracle whose output is truncated to $n$ bits. This implies the resistance to the traditional hash function attacks, such as $2^{n/2}$ for collision and $2^n$ for (second) pre-image attacks.

For cryptographic primitives with variable-length output, such as RadioGatún, expressing the required resistance with respect to the output length makes little sense as this would imply that it should be possible to increase the security level indefinitely by just taking longer outputs. Rather than claiming resistance levels against the traditional hash function attacks, we decided to express the security claim as what an ideal function could achieve. In the paper on RadioGatún, we proposed for that purpose something we called an ideal mangling function. However, after publication we noticed that this was not ideal and we decided to dig more deeply into this subject. Our goal was to specify a function that behaves like a random oracle, with the sole exception that it would have inner collisions. This search led to so-called random sponge functions. The results of this initial search was presented at the Dagstuhl seminar on Symmetric Cryptography in January 2007, and soon after the final definition of sponge functions was given at the Ecrypt Hash Workshop in Barcelona.

The sponge construction

The sponge construction is a simple iterated construction for building a function $F$ with variable-length input and arbitrary output length based on a fixed-length permutation (or transformation) $f$ operating on a fixed number $b$ of bits. Here $b$ is called the width.

The sponge construction operates on a state of $b=r+c$ bits. The value $r$ is called the bitrate and the value $c$ the capacity.

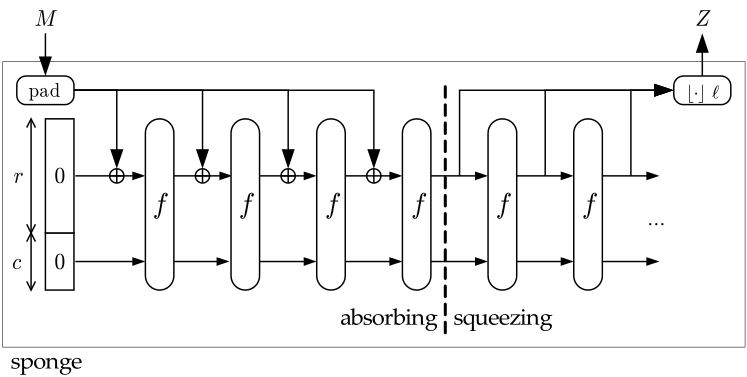
The sponge construction

First, the input string is padded with a reversible padding rule and cut into blocks of $r$ bits. Then the $b$ bits of the state are initialized to zero and the sponge construction proceeds in two phases:

• In the absorbing phase, the $r$-bit input blocks are XORed into the first $r$ bits of the state, interleaved with applications of the function $f$. When all input blocks are processed, the sponge construction switches to the squeezing phase.
• In the squeezing phase, the first $r$ bits of the state are returned as output blocks, interleaved with applications of the function $f$. The number of output blocks is chosen at will by the user.

The last $c$ bits of the state are never directly affected by the input blocks and are never output during the squeezing phase.

Sponge as a reference of security claims

One could exhaustively list all the properties that a hash function should resist to and assign them resistance levels. Alternatively, claiming the security of a concrete function with regard to a model means comparing the success probability of an attack on the concrete function against that on the model. This allows compact security claims, which address all the possible properties at once, including future requirements not foreseen in an exhaustive list.

In fixed digest-length hash functions, the required resistance against attacks is expressed relative to the digest length. Until recently one has always found it reasonable to expect a hash function to be as strong as a random oracle with respect to the classical attacks. However, this changed after the publication of the generic attacks such as multicollisions [Joux, Crypto'04], second pre-images on $n$-bit hash functions for much less than $2^n$ work [Kelsey and Schneier, Eurocrypt'05], herding hash functions and the Nostradamus attack [Kohno and Kelsey, Eurocrypt'06].

An iterated function uses a finite memory to store its state and processes the input, block per block. At any point in time, the state of the iterated function summarizes the input blocks received so far. Because it contains a finite number of bits, collisions can happen in this state. Random oracles, on the other hand, do not have collisions in their “state” as such a concept does not exist. This is the main reason for which random oracles cannot be used directly to express security claims of functions with variable-length output: they would simply never exhibit any effects of the finite memory any concrete iterated function has.

Random sponges functions, on the other hand, provide an alternative to the random oracle model for expressing security claims. A random sponge is an instance of the sponge construction with $f$ chosen randomly from the set of transformations (or of permutations) over $b$ bits. We have proven that a random sponge function is as strong as a random oracle, except for the effects induced by the finite memory. A random sponge can serve as a reference model for expressing compact security claims for iterated hash functions and stream ciphers.

When using a random sponge as a security reference, one considers the success of a particular attack. Such a success probability depends not only on the nature of the attack considered but also on the chosen parameters of the random sponge, i.e., its capacity, bitrate and whether it calls a random permutation or a random transformation. The flat sponge claim is a simplification in the sense that we consider only the worst-case success probability, determined by the upper bound on the random oracle differentiating advantage [Bertoni et al., Eurocrypt'08], which depends solely on the capacity of the random sponge. Hence, it flattens the claimed success probabilities of all attacks using a single parameter: the claimed capacity $c_{claim}$.

Sponge as a design tool

On top of its original goal as a security reference, we realized that the sponge construction could also be used to build efficient cryptographic primitives. An important aspect is that the cryptographic primitive to be designed is a fixed-length permutation rather than harder-to-build structures such as block ciphers or dedicated compression functions. This is rather good news in itself, as all the symmetric cryptographic services can be realized using only a single primitive: a fixed-length permutation. As opposed to a block cipher, a fixed-length permutation makes no distinction between data and key input and hence can treat all input bits on an equal footing and at the same time can be made simpler.

Generic attacks are attacks that do not exploit the properties of the concrete primitive but only the properties of the construction. The indifferentiability framework provides us with a way to upper bound the success probability of any single-stage generic attack [Maurer et al., TCC'04]. More concretely, we used it to prove that that the success probability of any generic attack to a sponge function is upper bound by its success probability for a random oracle plus $N^2/2^{c-1}$ with $N$ the number of queries to $f$. In fact, these results show that any attack against a sponge function implies that the permutation it uses can be distinguished from a typical randomly-chosen permutation. This naturally leads to the following design strategy, which we called the hermetic sponge strategy: adopting the sponge construction and building an underlying permutation f that should not have any properties exploitable in attacks. We have called such properties structural distinguishers.

In this approach, one designs a permutation $f$ on $b=r+c$ bits and uses it in the sponge construction to build the sponge function $F$. In addition, one makes a flat sponge claim on $F$ with a claimed capacity equal to the capacity used in the sponge construction, namely $c_{claim} = c$. In other words, the claim states that the best attacks on $F$ must be generic attacks. Hence, $c_{claim}=c$ means that any attack on $F$ with expected complexity below $2^{c/2}$ implies a structural distinguisher on $f$, and the design of the permutation therefore attempts to avoid such distinguishers. Note that the existence of a structural distinguisher for $f$ does not necessarily imply an attack or weakness in $F$. For example, any distinguisher for $f$ that has success probability zero below $2^{c/2}$ forms no threat, as the flat sponge claim expresses no security against adversaries that may send more than $2^{c/2}$ queries.

In the hermetic sponge strategy, the capacity determines the claimed level of security, and one can trade claimed security for speed by increasing the capacity $c$ and decreasing the bitrate $r$ accordingly, or vice-versa. When a padding rule is used with particular properties, one can securely instantiate sponge functions with different rates with the same fixed-length permutation. The simplest padding rule satisfying these properties is called the multi-rate padding: it appends a single 1-bit, then a variable number of zeroes and finally another 1-bit.

Fixed-length permutation as a versatile cryptographic primitive

With its arbitrarily long input and output sizes, the sponge construction allows building various primitives such as a hash function, a stream cipher or a MAC. In some applications the input is short (e.g., a key and a nonce) while the output is long (e.g., a key stream). In other applications, the opposite occurs, where the input is long (e.g., a message to hash) and the output is short (e.g., a digest or a MAC).

Another set of usage modes takes advantage of the duplex construction, a construction that is closely related to the sponge construction and whose security can be shown to be equivalent. The duplex construction allows the alternation of input and output blocks at the same rate as the sponge construction, like a full-duplex communication. This allows one to implement an efficient reseedable pseudo random bit sequence generation and an authenticated encryption scheme requiring only one call to $f$ per input block.

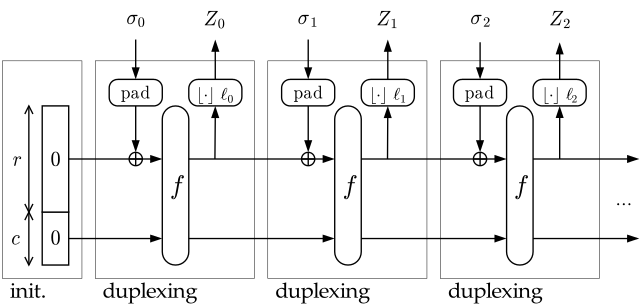
The duplex construction