Team Keccak
Guido Bertoni3, Joan Daemen2, Seth Hoffert, Michaël Peeters1, Gilles Van Assche1 and Ronny Van Keer1
1STMicroelectronics - 2Radboud University - 3Security Pattern
Home
Welcome to the web pages of the Keccak Team!
In these pages, you can find information about our different cryptographic schemes and constructions, their specifications, cryptanalysis on them, the ongoing contests and the related scientific papers.
Latest news
-
Halving the number of rounds in a primitive is quite unusual, if not unprecedented. Do you imagine shortening AES-128 from 10 down to 5 rounds? Dividing by two the number of steps in SHA-256? Using a 128-bit elliptic curve instead of Ed/X25519? Or cutting in half the dimensions of the ring in ML-KEM? In these cases, the security would be seriously questioned or even fall apart completely.
RFC 9861 defines two families of extendable output functions, both based on the Keccak-p[1600] permutation with 12 rounds, while the original SHA-3 and SHAKE family uses 24 rounds. Such a drastic reduction in the number of rounds may seem frightening, yet there is ample evidence from third-party cryptanalysis that 12 rounds provides a comfortable safety margin. For instance, the best collision attack reaches only 6 rounds. Despite its relative young age (it was first published in 2008), Keccak has been heavily scrutinized: The number of scientific papers that analyze it is higher than any other (unbroken) hash function!
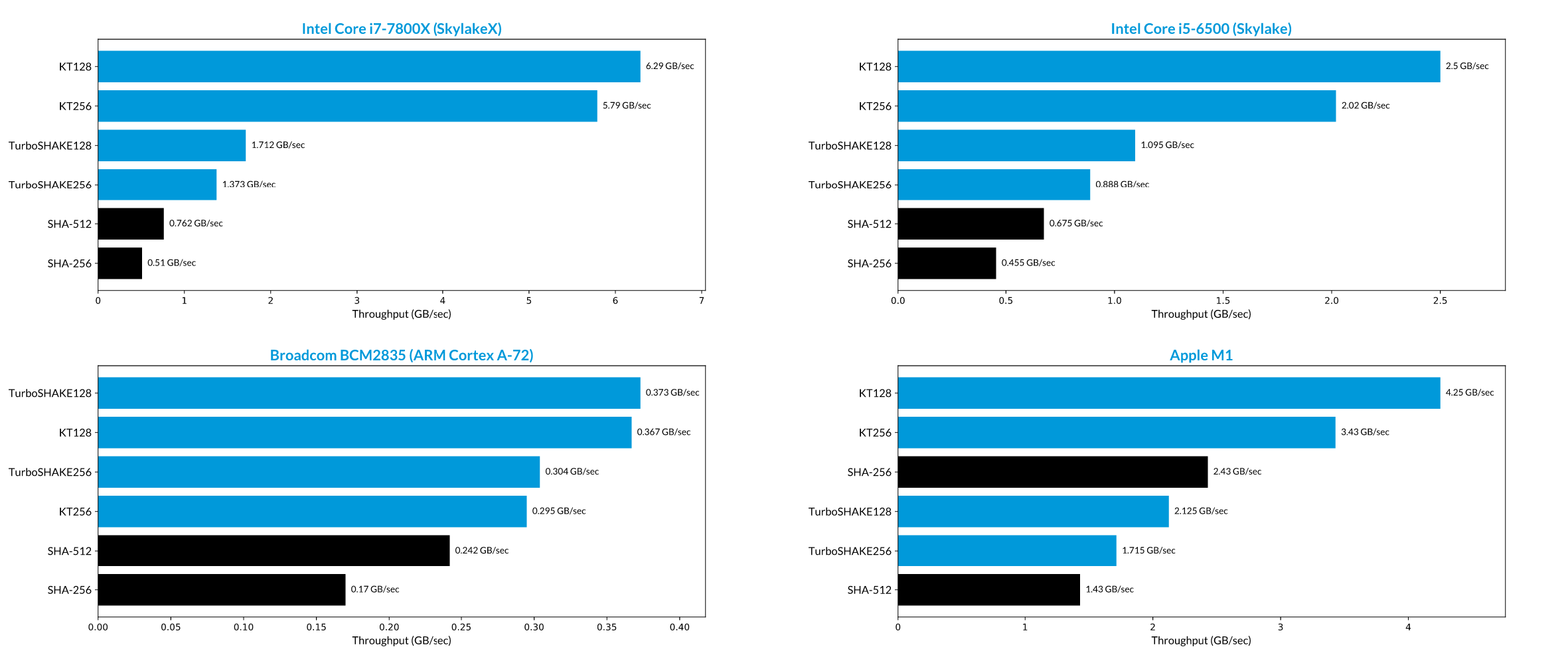
By halving the number of rounds, TurboSHAKE128 and TurboSHAKE256 hash twice as fast as SHAKE128 and SHAKE256, respectively. KT128 and KT256 further build upon these by adding parallelism to speed up the implementations even more. As a result, these functions are blazing fast, both in software and in hardware.
In the charts above, we show the throughput of the four functions defined in RFC 9861, plus SHA-256 and SHA-512, on four different processors. The Apple M1 has hardware acceleration for SHA-2 and SHA-3, which is used in our benchmark.
We first proposed KT128 in 2016 under the name KangarooTwelve. We then proposed it to the the Crypto Forum Research Group (CFRG) as an RFC draft in 2017. This was the start of a long process. TurboSHAKE is the sponge function underlying KangarooTwelve, but it got that name only in 2023, as we found it was an interesting function on its own. KangarooTwelve was then instantiated in two security levels, KT128 and KT256. Finally, the RFC was officially published in October 2025.
-
We congratulate Xiaoen Lin, Hongbo Yu, Chongxu Ren, Zhengrong Lu and Yantian Shen of Tsinghua University, Beijing, China, for solving the 4-round pre-image challenge on Keccak[r=240, c=160].
The previous pre-image challenge on the 400-bit version was solved on 3 rounds by Yao Sun and Ting Li in 2017. The solution to the present challenge was obtained using a meet-in-the-middle (MitM) involving symmetric states. The team reports a total complexity of about 258.7 4-round Keccak-f calls. It took about 4 days on the Sunway TaihuLight supercomputer using 10 thousand cores!
-
Started in June 2011, the Crunchy Contest proposes concrete collision and pre-images challenges based on reduced-round Keccak. After about 13 years, it is still active and the recent months have seen new challenges being solved. Hence, we would like to congratulate the authors of the latest solutions:
-
We congratulate Xiaoen Lin1, Hongbo Yu1, Zhengrong Lu1 and Yantian Shen1 for solving the 2-round pre-image challenge on Keccak[r=40, c=160].
The previous pre-image challenge on the 200-bit version was solved on 1 round by Joan Boyar and Rene Peralta in 2013. This present challenge was solved by combining linear structures and symmetries within the lanes and exploiting sparsity of the round constants.
-
Furthermore, we congratulate Xiaoen Lin1, Hongbo Yu1, Congming Wei2, Le He3 and Chongxu Ren1 for solving the 4-round pre-image challenge on Keccak[r=640, c=160].
The previous pre-image challenge on the 800-bit version was solved on 3 rounds by Jian Guo and Meicheng Liu in 2017. The solution to the present challenge was made possible by a number of optimizations related to linear structures and made use of mixed-integer linear programming (MILP). The team reports a total complexity of 260.9 4-round Keccak-f calls.
-
Finally, we congratulate Andreas Westfeld4 for solving the 2-round collision challenge on Keccak[r=40, c=160].
The previous collision challenge on the 200-bit version was solved on 1 round by Roman Walch and Maria Eichlseder in September 2017. The solution to the present challenge targets the rounds 3 and 4 specifically, as it exploits the round constant that is zero for ir=3 in the 200-bit version.
- Department of Computer Science and Technology, Tsinghua University, Beijing, China
- Beijing Institute of Technology, Beijing, China
- School of Cyber Engineering, Xidian University, Xi'an, China
- Faculty of Informatics/Mathematics, HTW Dresden, Germany
-
-
Looking back at 2022, we further improved the bounds of differential and linear trails in Xoodoo. In the article Tighter trail bounds for Xoodoo available on the IACR Cryptology ePrint Archive, we report on the outcome of our new trail scan effort. The importance of trail bounds is not to be repeated; instead we refer to last year's news item for a discussion. As you can see in the table below, the lower bounds have been quite significantly improved.
Next to a description of the optimizations in our trail search code that allowed us to improve the bounds, in the article we also report on a set of trails that are extendable to an arbitrary number of rounds and as such provide upper bounds for the minimum weight of trails. We summarize the new lower and upper bounds for the weight of trails in the table below. The bounds are the same for differential and linear trails.
# rounds 1 2 3 4 5 6 8 10 12 Lower bounds 2 8 36 80 98 132 176 220 264 Upper bounds 2 8 36 80 120 168 288 440 624 -
Currently, the vast majority of symmetric-key cryptographic schemes are built as modes of block ciphers. What would cryptography look like if it was built around another primitive? In this note, we explain our approach to authentication, encryption and authenticated encryption using a primitive type that we call deck functions. For more details, we invite you to watch our presentation All on deck! at RWC 2020, read our paper Jammin' on the deck or see its presentation at Asiacrypt 2022.
What are deck functions?
A deck function stands for doubly extendable keyed cryptographic function. It is not a construction like sponge or farfalle; instead, a deck function is a primitive type, the same concept as a block cipher. A primitive type abstractly defines a functional and security interface to modes, where the latter can be specified and proven secure independent of the details of the underlying primitive.
In a nutshell, a deck function is a function that, when keyed with a secret key, is hard to distinguish from a random oracle. Instead, a block cipher is a function that, when keyed with a secret key, is hard to distinguish from a random permutation. While the latter is called (S)PRP security, the security concept for a deck function is called PRF security, i.e., taking a key and a string as input, it outputs seemingly random bits for an adversary who does not know the key.
Yet, to qualify as a deck function, it must satisfy some additional requirements. First, the data input takes the form of a sequence of binary strings instead of a single one, and the output depends on the sequence and not just the concatenation of input strings. Then, a deck function must implement efficient incrementality properties. Specifically, both the input and the output are extendable: By keeping state, appending an extra string to the input sequence costs only the processing of this extra string. Similarly, like an extendable output function (XOF), asking for more output bits should be efficient.
Do you have examples of deck functions?
A construction for building deck functions is farfalle, of which Kravatte and Xoofff are instances.
However, there is nothing that prevents from building deck function differently, in the same way that there are multiple ways to build a block cipher: A wide design space is waiting to be explored!
What can you do with deck functions?
Like for block ciphers, we can define deck function modes of use for authentication, encryption and various kinds of authenticated encryption (AE). For instance, in our paper, we describe five modes with different robustness properties. Four of these modes are variations around a Feistel network structure, with a consistent and unified approach. This Feistel network has two mandatory central rounds and two optional outer rounds. The central rounds provide AE with nonce-misuse robustness, while the optional round at the beginning reduces the ciphertext expansion and the optional round at the end adds resistance against release of unverified plaintext (RUP).
Building AE schemes with such properties is not new and can be done based on block ciphers, but in the case of deck functions, the modes become really simple and natural. Passing a sequence of input strings and supporting incremental inputs are key ingredients in this simplicity, see for instance Seth's article on modes and his recent paper Nonce-encrypting AEAD Modes with Farfalle.
Wait, aren't you just pushing the complexity down to the primitive?
It is true that with deck functions we move the burden of dealing with variable input and output lengths from the mode to the primitive. It turns out that this allows more efficient schemes. Traditionally, block cipher-based modes rely on their (S)PRP security, and achieving a solid level of (S)PRP security comes at the price of a relatively large number of rounds. On the other hand, building a variable-input-length function that targets PRF security using the same building blocks can be done more efficiently when the reductionist security argument is dropped. Think about how much faster Pelican-MAC is compared to AES-CMAC: The former needs 4 rounds per 128 bits of input when the latter needs 10!
Besides efficiency, what are other advantages of deck functions?
Their incrementality properties are particularly well suited for uses of AE that go beyond the encryption and/or authentication of individual messages. In particular, processing streams of data, with intermediate tags, and bi-directional communications benefit from simpler modes.
In this context, a session deals with the authentication of sequences of messages, preventing an attacker from reshuffling messages. Ensuring that a message is authenticated in the context of previously sent messages comes essentially for free thanks to the incrementality properties of deck functions. Another interesting use case is the transmission of long messages to low-end devices, where intermediate tags can authenticate the message in an incremental way.
Concretely, how can I start using deck functions?
It depends on what you want to do.
If you are implementing a new protocol, note that Kravatte and Xoofff are supported in the XKCP and in a few other places. Currently, Xoofff has our preference because of its efficiency on a wide range of platforms, from the low-end processors as used in embedded devices to the high-end server processors. On the ARM™ Cortex-M0 and -M3, Xoofff outperforms AES-based schemes by a factor 4 or 5, and with AVX-512 instructions it runs faster than AES-based schemes even with the dedicated AES instructions!
If you are interested in modes and in proving their security, you may want to adapt existing modes with interesting properties to deck functions and see if the deck function interface makes them simpler. If you are a cryptographic designer, maybe your favorite design approach can be applied to build a deck function. And if you are interested in cryptanalysis, you may want to have a critical look at farfalle, our schemes and possibly new deck functions.
The possibilities are endless!