Keccak is defined solely of operations on bits. When implemented on a typical computer, the input and output bits must be packed in bytes following a well-defined convention. In the case of Keccak, the convention is the little-endian convention, i.e., the first bit goes to the least significant bit position of a byte.

In more details, a n-bit string consists of a sequence of bits numbered from 0 (the first bit of the string) to n-1 (the last bit of the string). When packed into a byte or a word of n bits or less, bit number i goes to the position representing the coefficient of 2ⁱ in the byte's or the word's integer value. Conversely, a byte (or in general, a word of n bits) represents a string of bits numbered from 0 (the least significant bit, coefficient of 2⁰) to n-1 (the most significant bit, coefficient of 2^n-1).

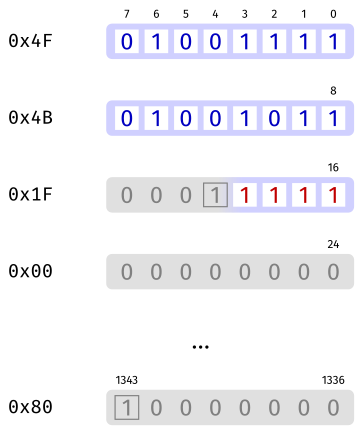
Let us illustrate this by hashing with SHAKE128 the two-letter string OK encoded in ASCII. The two bytes encoding OK are 0x4F followed by 0x4B, which represent the bit string 11110010 11010010. Then, SHAKE128 appends the suffix 1111 to that, since SHAKE128(“OK”) = Keccak[r=1344, c=256](“OK” || 1111). This gives the 20-bit string 11110010 11010010 1111, which are input to Keccak.

Inside Keccak, we pad the input using the pad10*1 rule to make a 1344-bit block. For this, we append a bit 1, then 1322 bits 0, then the final bit 1. This gives the following 1344-bit string depicted below.

Let us now reinterpret this block as bytes, as it would typically be stored. In the figure below, we can see the two letters encoded in ASCII, the delimited suffix d=0x1F for SHAKE128, a bunch of bytes 0x00 and finally the last byte 0x80.